1- Resuelve las siguientes ecuaciones de primer grado
1

2

3

4

5

6

7

8

9

10

2- Resuelve las siguientes ecuaciones de segundo grado
1

2

3

4

5

6

7

8x2 + (7 − x)2 = 25
97x2 + 21x − 28 = 0
10−x2 + 4x − 7 = 0
3-Resuelve por sustitución y igualación
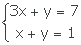
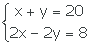
4-Resuelve por reducción
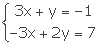
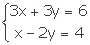
5 Resuelve por sustitución, igualación, reducción
y gráficamente el sistema:


6-Resuelve el siguiente problema por reducción
a)Pablo compra en una tienda de segunda mano un videojuego de fútbol y dos de boxeo por 55 €. Andrea compra en la misma tienda tres de fútbol y uno de boxeo por 90 €.
b)Una granja tiene pavos y cerdos, en total hay 58 cabezas y 168 patas. ¿Cuántos cerdos y pavos hay?
c)Antonio dice a Pedro: "el dinero que tengo es el doble del que tienes tú", y Pedro contesta: "si tú me das seis euros tendremos los dos igual cantidad". ¿Cuánto dinero tenía cada uno?